| Feigenbaum Constant Approximations | |
A curious approximation to the Feigenbaum constant ![]() is given by
is given by
| (1) |
where ![]() is Gelfond's constant, which is good to 6 digits to the right of the decimal point.
is Gelfond's constant, which is good to 6 digits to the right of the decimal point.
M. Trott (pers. comm., May 6, 2008) noted
| (2) |
where ![]() is Gauss's constant, which is good to 4 decimal digits, and
is Gauss's constant, which is good to 4 decimal digits, and
| (3) |
where ![]() is the tetranacci constant, which is good to 3 decimal digits.
is the tetranacci constant, which is good to 3 decimal digits.
A strange approximation good to five digits is given by the solution to
| (4) |
which is
| (5) |
where ![]() is the Lambert W-function (G. Deppe, pers. comm., Feb. 27, 2003).
is the Lambert W-function (G. Deppe, pers. comm., Feb. 27, 2003).
| (6) |
gives ![]() to 3 digits (S. Plouffe, pers. comm., Apr. 10, 2006).
to 3 digits (S. Plouffe, pers. comm., Apr. 10, 2006).
M. Hudson (pers. comm., Nov. 20, 2004) gave
| (7) | |||
| (8) | |||
| (9) |
which are good to 17, 13, and 9 digits respectively.
Stoschek gave the strange approximation
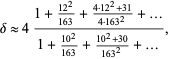 | (10) |
which is good to 9 digits.
R. Phillips (pers. comm., Sept. 14, 2004-Jan. 25, 2005) gave the approximations
| (11) | |||
| (12) | |||
| (13) | |||
| (14) | |||
| (15) | |||
| (16) |
where e is the base of the natural logarithm and ![]() is Gelfond's constant, which are good to 3, 3, 5, 7, 9, and 10 decimal digits, respectively, and
is Gelfond's constant, which are good to 3, 3, 5, 7, 9, and 10 decimal digits, respectively, and
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) | |||
| (23) |
which are good to 3, 3, 3, 4, 6, 8, and 8 decimal digits, respectively.
An approximation to ![]() due to R. Phillips (pers. comm., Jan. 27, 2005) is obtained by numerically solving
due to R. Phillips (pers. comm., Jan. 27, 2005) is obtained by numerically solving
| (24) |
for ![]() , where
, where ![]() is the golden ratio, which is good to 4 digits.
is the golden ratio, which is good to 4 digits.
No comments:
Post a Comment